26-то: Основният принцип на междурегионалните масиви
Част 1 Фалшив масив/псевдо масив (броене на подмножество)
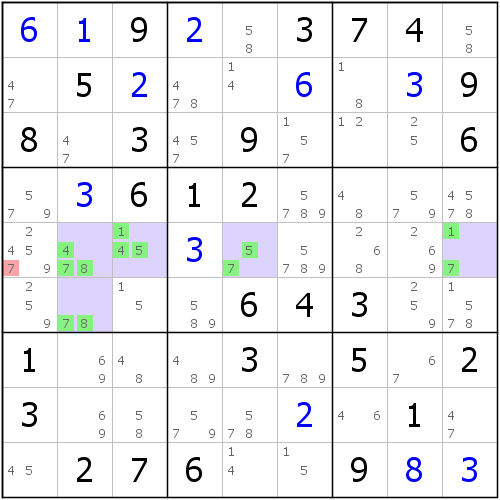
както е показано на снимката. Наблюдаваме петте клетки на R5C2359 и R6C2. Те имат магическо място, където само пет различни кандидата 1, 4, 5, 7 и 8 са само пет различни кандидата. Това отговаря на дефиницията на масива, но това група ли е? разбира се, не може да се определи директно. Дефиницията на масива е, че той трябва да бъде посочен в една и съща област и петте решетки тук включват междурегионална клетка, като R6C2 и R5C9 Два класа, ИЗОБЩО няма да бъдат свързани.
ТОГАВА НИЕ МИСЛИМ ЗА ТОЗИ ВЪПРОС: Тъй като ние сме много сходни с Array, тогава „Вътрешното попълване НЕ Е“ и „Вътрешните попълвания трябва да се повтарят“, за да обсъдим ситуацията.
Открихме, че петте числа от числата 1, 4, 5, 7 и 8 са ВЪЗМОЖНИ САМО ЗА ДА ИМАТ число 7, което може да се повтаря. Тъй като позицията на 7 може да бъде попълнена в R6c2 и R5c9 едновременно, . може да има дубликат Останалите числа обаче не могат да се повторят. Например, само позицията на 1 се появява в R5C39, само R5C39 партньори (R5), така че тези две мрежи може да имат само един от тях;. същото, 4 позиция Само в R5C23, само R5C23 Peers (R5) и Tong Palace (B4), ТАКА ЧЕ 4 в тази FIVED Е ПО-НЕВЪЗМОЖНА; Аналитичните методи 5 и 8 са едни и същи (5 Всички запълвания може би всички, запълванията от 8 могат да бъдат тонирани към двореца. Така че само цифровите 7 може да имат повторение.
ТАКА, АКО искате да попълните петте числа от 1, 4, 5, 7, 8 към тази петорка, КОГАТО ИМА, R5C9 и R6C2 са 7), останалите R5C235 три решетки, има четири попълнени Числа (1, 4, 5, 8) По избор. в този Wre, кои три числа бяха избрани и ние не знаехме. Така че в това отношение не можем да успеем. Но можем да определим, че независимо дали не се повтаря, числото 7 е незаменимо в структурата. с други думи, броят на тези четири решетки е невъзможно да изчезне от диска. В същото време, когато бъде премахнато, остават само четири числа (1, 4, 5, 8) в тази ПЕТ МРЕЖА, но тъй като те трябва да се повтарят, това очевидно не е достатъчно, ТАКА ЧЕ ЩЕ произведе противоречие., ТАКА ЩЕ СЕ ПРОИЗВЕДЕ.
Оттогава стигнахме до извода: без значение как числото е попълнено вътре, числото 7 е незаменимо, така че това, което се изтрива, е позицията, на която отговаря четиримата кандидат номер 7. Следователно, r5c1 <> 7.
Тази структура се нарича псевдо-масив (или фалшиво число, Extended Subset Principle / Subset Count. Псевдо-масивът е доста болезнен и е много труден, а заключението е толкова „безразсъдно“. Така е и там Някакъв по-прост начин? ИЛИ КАЖЕТЕ, Как да наблюдаваме и използваме по-бързо?
Част 2 Теорията и принципът на изтриването на междурегионален масив
Посоката на анализа на псевдо-масива обикновено е в съответствие с това дали е „междурегионален масив“. Ако е така, вътрешният не се повтаря;.. Ако не, трябва да има повтарящи се числа вътре След това отидете на числото за повторение до края Псевдо-масивът има функция Когато изведем принципа, той получи точка:... псевдо-масивът приема че вътре има повторение, единственият номер на повторение може да не изчезне от диска. Следователно, когато наблюдавате и намирате заключението, стига единственото число, което може да се прегледа, то може да бъде изтрито директно.
ЗНАЧИ, виждате ли го, ТОВА Е МЕЖДУРЕГИОНАЛНА СТРУКТУРА, НО ВЪТРЕ НЕ ТРЯБВА ДА СЕ ПОВТАРЯ? Някои, като този пример.
Както показва снимката. Спазвайте R34c34 Четири, Само 1, 4, 6, 8 Четири числа ВЪТРЕШНО И ПОПЪЛНЕТЕ ЧЕТИРИ. ОБАЧЕ ГЕНИАЛНО Е, че 1, 4, 6, 8 не се повтарят, защото всички позиции за запълване на числото 1 са равни, всички позиции за запълване на преминаването на номер 4, всички позиции за запълване на числото 6, всички пълнители В 8 местоположения връстници. Така че е невъзможно да има повтарящо се запълване.
Казахме, че ако анализирате псевдомасив, се установи, че той не се повтаря вътре, тази структура се нарича Разпределено разединено подмножество, наричано DDS, наричано кръстосано регионално поле. И така, какво трябва да изтрие DDS?
Поради вътрешни неповтарящи се връзки, масив от различни зони трябва да бъде попълнен само с тези числа, с други думи, тези числа са от съществено значение. Така, например, пример за запълване е представен на R34C4, останалите клетки не могат да бъдат 1; 6 от запълванията може да се появят на R4C34, така че останалите клетки в R4 не могат да бъдат 6, докато 4 и 8 са еднакви. Следователно броят на изтриванията е отбелязан на картата. Разбира се, този пример ИМА DDS, моля, потърсете ГО.
Част 3 SDC и разширен масив
SDC е особено обезпокоителен, който е разделен на много различни ситуации за обсъждане и анализ. В крайна сметка обаче открихме, че много „просто“ са доволни, като 1, 4 двойки, 2, 6, 7 три групи, 2, 6, 7, 2, 6, 7, 2, 6, 7 и това Отделно 9, всичко „се случва“. ТОЛКОВА МНОГО „САМО“, НАИСТИНА ЛИ Е ПРИЧИНЕНО? Сега нека да разгледаме този проблем.
Както е показано на фигурата, това е SDC, но не съм разделен на оранжево и зелено, за да рисувам. Защото това е по-близо до анализа на псевдомасива.
Ние използваме метода за анализ на псевдо-масив, ТОВА Е междурегионален седем масив, но умно е това Theled 1, 2, 3, 4 колона (C8) и 7, 8 9 Tong Palace (B6), SO това е ддс. според принципа на изтриване на DDS, останалите клетки в C8 не трябва да бъдат 1, 2, 3, 4; И останалите клетки в B6 не могат да бъдат 7, 8, 9. Затова ги изтривам.
НАБЛЮДЕНИЕТО НА SDC може да бъде по-проблемно, тъй като са необходими две области за поемане на случая, КЪДЕТО ВИЕ ОПРЕДЕЛИХТЕ. Но използвайте псевдомасива, малко по-лесно ли е?
Fusion-to-Range (SDC) ИМА име, наречено Two-Sector Disjoint Subset поради тази причина.








