Salaus - Bag Algorithm for Public Key Cryptography System 1

Cipher - Bag Algorithm for Public Key Cryptography System 1

Kuten me kaikki tiedämme, julkisen avaimen salasana, joka tunnetaan myös epäsymmetrisenä salasanana, on yleisempi seuraavien kolmen matemaattisen ongelman perusteella:

Suurten tekijöiden hajoamisen vaikeudet (RSA)

Erillinen uuttopari (ELGAMAL)

Elliptinen käyrä, joka ratkaisee ongelman (ECC)

Tämä johdanto ei ole edellä mainittuja kolmen tyyppisiä julkisen avaimen salausjärjestelmiä, mutta ennen kuin julkisen avaimen salasana tulee näkyviin, julkisen salasanan salausalgoritmi on olemassa, reppualgoritmi; reppualgoritmi on Merklen ja Hellmanin kehittämä reppualgoritmi. Sitä voidaan käyttää vain salaukseen, ja sitten shamir parantaa sitä, jotta se on käytettävissä digitaalisia allekirjoituksia varten;

Reppualgoritmin turvallisuus sai alkunsa reppuongelmasta, hän on täysi kysymys NP:stä, mutta myöhemmin selvisi, että algoritmi ei ole turvallinen, mutta koska se todistaa kuinka käyttää NP-täysi ongelmia julkiseen salasanaan, kannattaa oppimista.

Tässä on reppualgoritmi: Kuvaus: jos tavara on erilainen, jokainen paino on erilainen, voiko reppuun laittaa muutaman kappaleen näistä esineistä, jotta se vastaa tiettyä painoa? Kaavan kuvaus: Kun annetaan sarja arvoja M1, M2, ..., Mn ja S-arvo, laske BI, joka tyydyttää: s = b1 + b2m2 + ... + bnmns = b1m1 + b2m2 + ... + bnMnbibi-arvo Se voi olla 0, 1,1, mikä tarkoittaa, että tämä esine on repussa, 0 tarkoittaa sitä;

Yksinkertaisen esimerkin antamiseksi: Nämä esineet voivat painaa 1, 5, 6, 11, 14, 20, ne voidaan koota repuksi, jossa on 5, 6 ja 11, eikä reppu, joka on koottu 24:ksi, ei ole mahdollista. Yleisesti ottaen tämän ongelman ratkaisemiseen tarvittava aika näyttää pidentyneen eksponentiaalisesti kohteiden määrän kasvaessa;

Merkle-Hellman-reppualgoritmin ideana on koodata viesti reppuongelman ratkaisuksi. Suunnitelman pituus on yhtä suuri kuin kasan kohteiden lukumäärä ja kirkas teksti vastaa B:n arvoa, ja salateksti lasketaan ja arvo lasketaan, ja seuraavassa kuvassa on seuraavan esimerkin kappale salaukseen ;

Reppu on itse asiassa olemassa kahdessa eri reppuongelmassa:

Lineaarinen aika voidaan ratkaista;

Lineaarinen aika ei ole käytettävissä. helppo ratkaista reppuongelma voidaan muuttaa vaikeaksi reppuongelmaksi. Julkinen avain käyttää vaikeaa reppuongelmaa, se voidaan helposti dokumentoida, mutta salatekstiä ei ole mahdollista purkaa, yksityisiä salaisuuksia käytetään helposti reppuongelman ratkaisemiseen, hän antaa yksinkertaisen salauksen purkumenetelmän. Ihmisten, jotka eivät tiedä, täytyykö yksityisten avainten murtaa salatekstit, heidän on ratkaistava harvinainen reppuongelma.

Helppojen ratkaisujen saamiseksi voit valita ylihinnan, jolloin vastaava reppuongelma on helppo ratkaista. Selvittävä sekvenssi: Se on suurempi kuin se, esimerkiksi {1, 3, 6, 13, 27, 52} on supersekvenssi, ja {1, 3, 4, 9, 15, 25} ei ole.

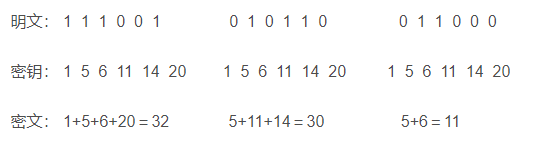
Yliinkrementaalisen repun ongelman ratkaisu on helppo löytää, laskea sen kokonaismäärä ja verrata sarjan maksimilukua, jos kokonaispaino on pienempi kuin tämä luku, se ei ole repussa, jos kokonaismäärä paino on tätä suurempi, se on repussa, reppu Paino vähennetään sarjan seuraavan maksimiluvun tutkimiseksi, toista loppuun asti. Jos kokonaispaino pienennetään nollaan, on vain yksi ratkaisu, muuten ratkaisua ei ole.

例如，总重量为70的一个背包，超递增序列为{2，3，6，13，27，52}；最大重量为52，小于70，所以52在背包中，70-52 = 18，下一个重量27 >18，因此，27不在背包中，在下一个13<18，13在背包中，18-13 = 5，以此类推，再下一个，3与2均在背包中，总重量减为0，表明已求出一个解，如果这个一个M-H背包加密分组，那么对应的密文70的解为110101.

Ei-superinkrementaalisen sekvenssin reppu on vaikea, niillä ei ole nopeaa algoritmia. Päättääksesi, kumpi repussa on, testaa kaikkia ratkaisuja vuorotellen, kunnes saat oikean ratkaisun. Nopeimmalla algoritmilla on edelleen vaikeuksia lisätä ongelmia repussa, jälkimmäiselle, kun liityt sekvenssiin, ratkaiseminen tarvitsee vain tehdä toisen toiminnon.

Merkle-Hellman-reppualgoritmi käyttää tätä luonnetta. Yksityinen ydin on painosarja, joka lisää reppuongelmia. Julkinen avain on sarja tavallisia reppuongelmia, Merkle ja Hellman suunnittelivat menetelmän muuntaa yli-inkrementaaliset reppuongelmat tavallisiksi reppuongelmiksi, jotka käyttävät mallinlaskentaa tämän muutoksen suorittamiseen.

Jälkeenpäin julkisen salaisen avaimen luominen yksityisellä avaimella: ota inkrementaalinen sekvenssi, kuten {2, 3, 6, 13, 27, 52}, jossa n - ota kaikki kohteet ja tee sitten moodinumerot M:llä. Moduulin tulee olla suurempi kuin sekvenssin kaikkien numeroiden lukumäärä, kuten 105. Kertoimen tulee olla minkä tahansa sekvenssin numeron kanssa, kuten 31. Siksi, yleinen reppujärjestys on:

2 * 31 mod105 = 623 * 31 mod105 = 936 * 31 mod105 = 8113 * 31 mod105 = 8827 * 31 mod105 = 10252 * 31 mod105 = 37

Siksi saatu reppu on {62, 93, 81, 88, 102, 37}. Superinkrementaalinen reppusekvenssi on yksityinen avain, ja saatu reppusekvenssi on avoin salainen avain.

Jos haluat salata binääriviestin, jaa se ensin useiksi paketeiksi, jotka on kuvattu reppusarjassa. Sitten käytetään numeroa 1 esittelemään esine, mikä osoittaa, että tuotetta ei ole olemassa, ja laskee repun kokonaispainon. Toista tämä toimenpide kaikille paketeille. Jos viesti on esimerkiksi binäärinumero 0110001101101101110, salausprosessi käyttämällä yllä olevaa reppualgoritmia on seuraava:

Uutiset = 011000 110101 10110011000 Kirjeenvaihto 93 + 81 = 17411010 vastaa numeroa 62 + 93 + 88 + 37 = 280101110 Kirjeenvaihto 62 + 8 = 3 +2 8 = 3 +1

Siksi Ciphet on 174, 280, 333

Vastaanottaja yksityiseen salaiseen avaimeen asti: Alkuperäistä superinkrementtireppua käytetään sen muuntamiseen N:n ja M:n arvoiksi yleisissä repuissa. Viestin salauksen purkamiseksi vastaanottajan on ensin laskettava N ^ {- 1} n-1, jotta se täyttää n * n ^ {- 1} == 1 mod mn * n-1 == 1MODM. Käytä n ^ {- 1} N-1-tilaa M kerro teksti jokaisen esineen arvolla ja käytä sitten yksityisiä reppuja sen jakamiseen.

Tässä esimerkissä superinkrementaalinen reppu: {2, 3, 6, 13, 27, 52} m = 105, n = 31, salatekstiviesti on 174, 280, 333. n ^ {- 1} = 61n-1 = 61, joten salatekstin arvo on kerrottava 61:llä 105. 174 * 61 MOD 105 = 9 = 3 + 6 vastaavuus 0111000; 280 * 61 mod 105 = 70 = 2 + 3 + 13 + 52 vastaa 110101; 333 * 61 mod 105 = 48 = 2 + 6 + 13 + 27 kirjeenvaihto 0111000; Siksi seuraavasta tekstistä numeroon 011000 110101 101110 käy selväksi

Vain 6 reppusarjan ratkaiseminen ei ole kovin vaikeaa, vaikka sama järjestys on sama. Varsinaisen reppualgoritmin tulee sisältää vähintään 250 esinettä. Superinkrementaalisessa repussa kukin arvo on yleensä 200 - 400. Moduuli on yleensä 100 - 200. Tätä algoritmia käytetään todellisessa käytössä, ja satunnaissekvenssigeneraattori luo nämä arvot.

Tällaiselle repulle on hyödytöntä yrittää käyttää uupumushyökkäystä sen hajottamiseksi. Vaikka tietokone voisi laskea miljoona kertaa sekunnissa, kokeile kaikkia mahdollisia reppumatkailijoita, 10 ^ {46} 1046.

Koska sanotaan, että vaikka pakokaasuhyökkäysten käyttöä ei voidakaan tulkita, miksi tämä algoritmi on todistettu tai murrettu? Osa SHAMIR-kuluista, reppualgoritmi voidaan purkaa ja asiaan liittyvä kirjallisuus löytyy.