26th: The Basic PrinciPle of Cross-Regional Arrays
Part 1 Fake Array/Pseudo Array (Subset Counting)
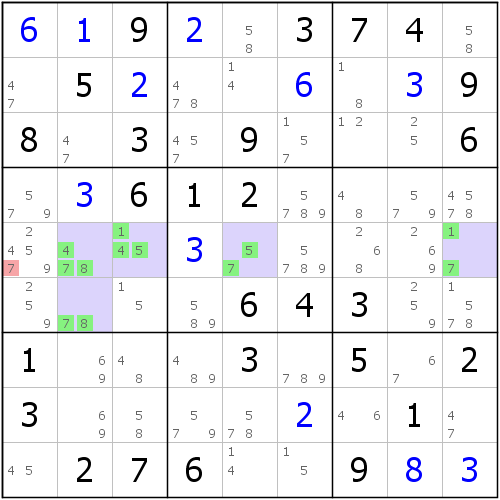
as the picture shows. We observe the five cells of R5C2359 and R6C2. They have a magical place that just five different candidates 1, 4, 5, 7, and 8 are just five different candidates. This happens to meet the definition of the array , but is this a group? of course, it can not be determined directly. The definition of the array is that it must be specified in the same area, and the five grids here include a cross-regional cell, such as R6C2 and R5C9 Two classes, IT Will Not Be Associated At ALL.
THEN WE THINK THIS Question: Since We are Very Similar TO Array, Then "Internal Filling Does NOT" And "Internal Fills Have Repeat" to Discuss The Situation.
We Found That The Five Numbers of Numbers 1, 4, 5, 7, and 8 Are ONLY POSIBLE TO HAVE A Number 7 May Be Repeated. Because The position of the 7 Can Be Filled in The R6c2 And R5c9 At The Same Time, The . may have duplicate However, the remaining numbers are not possible to repeat For example, only the position of 1 appears in R5C39, just R5C39 peers (R5), so these two grids may only have one of them;. the same, 4 position Only In R5C23, Just R5C23 Peers (R5) And Tong Palace (B4), SO 4 in this FIVED IS More Impossible; The 5 and 8 Analytical Methods Are The Same (5 All Fills Maybe All, The Fills of 8 May Be Toned To The Palace. So Only Digital 7 May Have Repetition.
SO, IF you want to fill in The Five Numbers of 1, 4, 5, 7, 8 to this Five-Piece, WHEN THERE, R5C9 and R6C2 Are 7), The Remaining R5C235 Three Grids, There Are Four Filled Numbers (1, 4, 5, 8) Optional. in this Wre, Which Three Numbers Were Selected, And We Didn't Know. So in this Regard, We can't make it it. But we can determine That no matter whether it is not repeated, the number 7 is indispensable in the structure. in other words, the number of these four grids is impossible to disappear from the disk. At the same time, when it is removed, there are only four numbers (1, 4, 5, 8) Left in this FIVE GRID, But Because They Must Be Repetitive, this is obviously not enough, SO IT WILL Produce Contradiction., SOI IT WILL CONTUCE.
Ever since, we have come to the conclusion: no matter how the number is filled inside, the number 7 is indispensable, so what is deleted is the position that the four candidate number 7 corresponds to. Therefore, r5c1 <> 7.
This structure is called a pseudo-array (or false number, Extended Subset PrinciPle / Subset Count. The pseudo-array is quite painful, and it is very hard, and the conclusion is so "grass rate". So is there any way simpler ? OR SAY, How to Observe and Use Faster?
Part 2 The theory and principle of cross-area array deletion
The analysis direction of the pseudo-array is generally in accordance with whether it is a "cross-regional array" If so, the inside is not repeated;.. If not, there must be repeated numbers inside Then go to the repetition number to the end The pseudo-array has a feature When we derive the principle, it got a point:... the pseudo-array assumes that there is repetition inside, the only number of repetition may not disappear from the disk Therefore, when observing and Finding the conclusion, as long as the only reviewable number is, it can be deleted Directly.
SO, Do You See It, IT IS A CROSS-Regional Structure, But INSIDE MUST NOT Repeat? Some, Such As this Example.
As The Picture Shows. Observe R34c34 Four, Only 1, 4, 6, 8 Four Numbers INTERLY, AND FILL IN FOUR. HOWEVER, Ingenious IS That 1, 4, 6, 8 IS Not Repetitive, Because All The Fill Positions of the Number 1 Are Equal, All of the Fill Positions of the Numr 4 Pass, All The Filling Positions of The Number 6, All Fillers In 8 location peers. So this is impossable to have a repitive fill.
We said that if you analyze a pseudo-array, it is found that it is not repeated inside, this structure is called Distributed Disjointed Subset, referred to as DDS, referred to as a cross-region array. So what should a DDS deletion?
Due to internal non-repetitive relationships, a cross-zone array must only be filled in these numbers, in other words, these numbers are essential. Thus, for example, an example of the fill is presented on R34C4, the remaining cells can not be 1; 6 of the Fills May Appear on the R4C34, SO The Remaining Cells in R4 Are Not Can Be 6, While 4 and 8 Are The Same. Therefore, The Number of Deletions Has Been Labled On The Map. Of Course, this Example HAS A DDS, Please Look for IT.
Part 3 SDC and spanned array
SDC is particularly troublesome, which is divided into many different situations to discuss and analyze. However, in the end we found that many "just" satisfied, such as 1, 4 pairs, 2, 6, 7 three groups, 2, 6, 7, 2, 6, 7, 2, 6, 7, and this Separate 9, IT IS all "happens to". SO MANY "JUST", IS IT Really Caused? Now Let's Take a Look At this Problem.
AS Shown In The Figure, This Is AN SDC, But I am Not Divided Into Orange and Green To Paint. Because this is closer to the analysis of the pseudo-array.
We use the pseudo-array analysis method, IT IS A Cross-Regional Seven Array, But Clever Is this Theled 1, 2, 3, 4 Column (C8), And 7, 8 9 Tong Palace (B6 ), SO it is dds. according to the principle of deletion of DDS, The Remaining Cells in The C8 Should Not Be 1, 2, 3, 4; And The Remaining Cells in B6 Cannot Be 7, 8, 9. So i delete Them.
THE OBSERVATION OF THE SDC May Be More TroubleSome, Because Two Areas Are Required To Assume The Case WHERE THEE DETERMINED. But Use the pseudo-array, is it slightly easier?
The Fusion-To-Range (SDC) HAS A Name Called Two-Sector Disjoint Subset Because of this Reason.
Latest: Second-hand iPad price / price purchase analysis
Next: BM (cochlear base film)








