Cipher - Bag Algorithm for Public Key Cryptography System 1
Cipher - Bag Algorithm for Public Key Cryptography System 1
As we all know, public key password, but also known as an asymmetric password, is more common based on the following three math issues;
Difficulties of large factors decomposition (RSA)
Discrete pair of extractance (ELGAMAL)
Elliptic curve discrete to nurse solve the problem (ECC)
1.背包算法This introduction is not the above three types of public key cryptosystems, but before the public key password appears, the public password encryption algorithm exists, the backpack algorithm; the backpack algorithm is the backpack algorithm developed by Merkle and Hellman. It can only be used for encryption, and then it will be improved by shamir to make it available for digital signatures;
The safety of the backpack algorithm originated in a backpack problem, he is a full question of NP, but later discovered that the algorithm is not safe, but because it proves how to use NP full problems to publicly password, it is worth learning.
Here is what is a backpack algorithm: Description: given an item, each weight is different, can put a few pieces in these items into a backpack, make it equal to a given weight? Formula Description: Given a series of values M1, M2, ..., Mn, and a S value, calculate BI, satisfying: s = b1 + b2m2 + ... + bnmns = b1m1 + b2m2 + ... + bnMnbibi value It can be 0, 1.1, indicating that this item is in the backpack, 0 means it;
To give a simple example: These items may weigh 1, 5, 6, 11, 14, 20, can be assembled into a backpack with 5, 6, and 11, and the backpack assembled to be 24 is not possible. In general, the time required to solve this problem seems to have exponentially increase with the increase of the number of items;
The idea of the Merkle-Hellman backpack algorithm is to encode the message as a solution of the backpack problem. The plan length is equal to the number of items in the heap, and the bright text is corresponding to the value of B, and the ciphertext is calculated and the value is calculated, and the following figure shows a paragraph of the following example to encryption;
The backpack actually exists in two different backpack issues:
Linear time can be solved;
Linear time is not available; easy to solve the backpack problem can be modified into a difficult backpack problem. Public key uses a difficult backpack problem, it can be easily used to documented, but it is not possible to decrypt ciphertext, private secrets use easy to solve the backpack problem, he gives a simple method of decryption. People who don't know if private keys must crack ciphertexts, they must solve a rare backpack problem.
2.超递增背包For easy solutions, you can choose overcharge, then the corresponding backpack problem is easy to solve. Overcoming sequence: It is greater than that of it, for example, {1, 3, 6, 13, 27, 52} is a super-sequence, and {1, 3, 4, 9, 15, 25} is not.
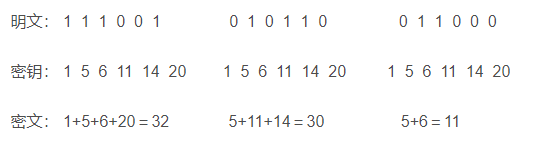
The solution of the over-incremental backpack problem is easy to find, calculate its total amount and compare the maximum number in the sequence, if the total weight is less than this number, it is not in the backpack, if the total weight is greater than this, it is in the backpack, backpack The weight will be subtracted to investigate the next maximum number in the sequence, repeat until the end. If the total weight is reduced to 0, then there is only one solution, otherwise, no solution.
例如,总重量为70的一个背包,超递增序列为{2,3,6,13,27,52};最大重量为52,小于70,所以52在背包中,70-52 = 18,下一个重量27 >18,因此,27不在背包中,在下一个13<18,13在背包中,18-13 = 5,以此类推,再下一个,3与2均在背包中,总重量减为0,表明已求出一个解,如果这个一个M-H背包加密分组,那么对应的密文70的解为110101.
The backpack of non-super-incremental sequence is difficult, they have no fast algorithm. To decide which one in the backpack is to test all the solution in turn until you get the correct solution. The fastest algorithm still has difficulty in incrementing problems in the backpack, for the latter, when you join a sequence, solving only needs to make another operation.
The Merkle-Hellman backpack algorithm uses this nature. Private kernel is a weight sequence over increments backpack issues. The public key is a sequence of ordinary backpack issues, Merkle and Hellman designed a method to convert over-incremental backpack problems to ordinary backpack issues, which use model computing to complete this change.
3.私人秘钥产生公开秘钥Hereinafter, how to generate a public secret key by a private key: take a incremental sequence, such as {2, 3, 6, 13, 27, 52}, with n to take all items, and then use M to do mode numbers The modulus should be larger than the number of all numbers in the sequence, such as 105. The multiplier should be with any of the numbers in the sequence, such as 31. Therefore, the general backpack sequence is:
2 * 31 mod105 = 623 * 31 mod105 = 936 * 31 mod105 = 8113 * 31 mod105 = 8827 * 31 mod105 = 10252 * 31 mod105 = 37
Therefore, the obtained backpack is {62, 93, 81, 88, 102, 37}. The super incremental backpack sequence is a private key, and the obtained backpack sequence is an open secret key.
4.加密过程To encrypt a binary message, first divide it into a number of packets detailed in the backpack sequence. Then, 1 is used to present the item, indicating that the item does not exist, and calculates the total weight of the backpack. Repeat this operation for all packets. For example, if the message is a binary number 0110001101101101110, the encryption process using the above backpack algorithm is as follows:
News = 011000 110101 10110011000 Correspondence 93 + 81 = 17411010 corresponds to 62 + 93 + 88 + 37 = 280101110 Correspondeal 62 + 81 + 88 + 102 = 333
Therefore, Ciphet is 174, 280, 333
5.解密过程The recipient until the private secret key: The original super increment backpack is used to convert it to the value of N and M in general backpacks. In order to decrypt the message, the recipient must first calculate N ^ {- 1} n-1 to meet n * n ^ {- 1} == 1 mod mn * n-1 == 1MODM. Use n ^ {- 1} N-1 mode M multiply text worth each item, and then use private backpacks to divide it.
In this example, the super incremental backpack: {2, 3, 6, 13, 27, 52} m = 105, n = 31, the ciphertext message is 174, 280, 333. n ^ {- 1} = 61n-1 = 61, so the ciphertext value must be multiplied by a 61 die 105. 174 * 61 MOD 105 = 9 = 3 + 6 correspondence 0111000; 280 * 61 mod 105 = 70 = 2 + 3 + 13 + 52 corresponds to 110101; 333 * 61 mod 105 = 48 = 2 + 6 + 13 + 27 correspondence 0111000; Therefore, it is clear from the following text to 011000 110101 101110
6.实际的实现方案To resolve only 6 backpack sequences is not very difficult, even the same sequence is the same. The actual backpack algorithm should at least contain 250 items. In the super incremental backpack, each value is generally 200 ~ 400. The modulus is generally 100 to 200. This algorithm is used in actual use, with a random sequence generator to generate these values.
For such a backpack, trying to use the exhaustion attack to decompose it is useless. Even if a computer can calculate 1 million times per second, try all possible backpackers, 10 ^ {46} 1046.
7.背包的安全性Since it is said that even if the use of exhaust attacks cannot be deciphered, why is this algorithm that is proved or cracked? Some of the SHAMIR spending, the backpack algorithm can be deciphered, and the relevant literature can be found.
Latest: [Kitbash3D] shop building construction street facilities 3D model package
Next: Jinkesen: 5.13 Gold Sitting on Crazy Roller Chat, CPI has a new high of more than 12 years








